المحتوى

• لتخطو
• جزء 1 من 4: رسم المصفوفة
• جزء 2 من 4: تعلم عمليات حل نظام بمصفوفة
• جزء 3 من 4: دمج الخطوات لحل المجرة
• جزء 4 من 4: فحص الحل
• نصائح

المصفوفة هي طريقة مفيدة جدًا لتمثيل الأرقام في شكل كتلة ، والتي يمكنك استخدامها بعد ذلك لحل نظام المعادلات الخطية. إذا كان لديك متغيرين فقط ، فمن المحتمل أن تستخدم طريقة مختلفة. اقرأ عن هذا في حل نظام المعادلات للحصول على أمثلة لهذه الطرق الأخرى. لكن إذا كان لديك ثلاثة متغيرات أو أكثر ، فإن المصفوفة مثالية. باستخدام مجموعات متكررة من الضرب والجمع ، يمكنك الوصول إلى حل بشكل منهجي.

لتخطو

جزء 1 من 4: رسم المصفوفة

1. تحقق من أن لديك بيانات كافية. للحصول على حل فريد لكل متغير في نظام خطي باستخدام مصفوفة ، يجب أن يكون لديك العديد من المعادلات مثل عدد المتغيرات التي تحاول حلها. على سبيل المثال: مع المتغيرات x و y و z تحتاج إلى ثلاث معادلات. إذا كان لديك أربعة متغيرات ، فأنت بحاجة إلى أربع معادلات.
   • إذا كان لديك معادلات أقل من عدد المتغيرات ، فستجد بعض حدود المتغيرات (مثل x = 3y و y = 2z) ، لكن لا يمكنك الحصول على حل دقيق. بالنسبة لهذه المقالة ، سنعمل فقط من أجل حل فريد.
2. اكتب معادلاتك في الصورة القياسية. قبل أن تتمكن من وضع البيانات من المعادلات في شكل مصفوفة ، عليك أولاً كتابة كل معادلة في شكل قياسي. الصيغة القياسية للمعادلة الخطية هي Ax + By + Cz = D ، حيث الأحرف الكبيرة هي المعاملات (الأرقام) ، والرقم الأخير (D في هذا المثال) على يمين علامة التساوي.
   • إذا كان لديك المزيد من المتغيرات ، فما عليك سوى متابعة السطر لطالما احتجت إلى ذلك. على سبيل المثال ، إذا كنت تحاول حل نظام به ستة متغيرات ، فسيبدو الشكل الافتراضي الخاص بك مثل Au + Bv + Cw + Dx + Ey + Fz = G. في هذه المقالة سوف نركز على الأنظمة ذات المتغيرات الثلاثة فقط. حل مجرة ​​أكبر هو نفسه تمامًا ، لكنه يستغرق المزيد من الوقت والخطوات.
   • لاحظ أنه في الشكل القياسي ، تكون العمليات بين المصطلحات دائمًا إضافة. إذا كان هناك طرح في المعادلة ، فبدلاً من الجمع ، سيكون عليك التعامل مع هذا لاحقًا بجعل المعامل سالبًا. لتسهيل تذكر ذلك ، يمكنك إعادة كتابة المعادلة وإضافة العملية وجعل المعامل سالبًا. على سبيل المثال ، يمكنك إعادة كتابة المعادلة 3x-2y + 4z = 1 بالشكل 3x + (- 2y) + 4z = 1.
3. ضع الأرقام من نظام المعادلات في مصفوفة. المصفوفة هي مجموعة من الأعداد مرتبة في شكل جدول ، وسنعمل من خلالها على حل النظام. يحتوي بشكل أساسي على نفس البيانات مثل المعادلات نفسها ، ولكن بتنسيق أبسط. لجعل مصفوفة معادلاتك في شكل قياسي ، ما عليك سوى نسخ المعاملات ونتيجة كل معادلة في صف واحد ، وتكديس هذه الصفوف فوق بعضها البعض.
   • افترض أن لديك نظامًا يتكون من ثلاث معادلات 3x + y-z = 9 ، 2x-2y + z = -3 ، و x + y + z = 7. سيحتوي الصف العلوي من المصفوفة على الأرقام 3 ، 1 ، -1 ، 9 ، فهذه هي المعاملات وحل المعادلة الأولى. لاحظ أن أي متغير ليس له معامل يُفترض أن يكون له معامل 1. يصبح الصف الثاني من المصفوفة 2 ، -2 ، 1 ، -3 والصف الثالث يصبح 1 ، 1 ، 1 ، 7.
   • تأكد من محاذاة معاملات x في العمود الأول ، ومعاملات y في العمود الثاني ، ومعاملات z في العمود الثالث ، وحدود الحل في العمود الرابع. عندما تنتهي من العمل بالمصفوفة ، ستكون هذه الأعمدة مهمة عند كتابة الحل.
4. ارسم قوسًا مربعًا كبيرًا حول المصفوفة بأكملها. حسب الاصطلاح ، تتم الإشارة إلى المصفوفة بزوج من الأقواس المربعة ، [] ، حول كتلة الأرقام بأكملها. لا تؤثر الأقواس على الحل بأي شكل من الأشكال ، لكنها تشير إلى أنك تستخدم المصفوفات. يمكن أن تتكون المصفوفة من أي عدد من الصفوف والأعمدة. في هذه المقالة ، سنستخدم الأقواس حول المصطلحات المتتالية للإشارة إلى أنها تنتمي معًا.
5. استخدام الرمزية الشائعة. عند العمل باستخدام المصفوفات ، من الشائع الإشارة إلى الصفوف التي بها الاختصار R والأعمدة ذات الاختصار C. يمكنك استخدام الأرقام مع هذه الأحرف للإشارة إلى صف أو عمود معين. على سبيل المثال ، للإشارة إلى الصف 1 من المصفوفة ، يمكنك كتابة R1. ثم يتحول الصف 2 إلى R2.
   • يمكنك الإشارة إلى أي موضع محدد في مصفوفة باستخدام مزيج من R و C. على سبيل المثال ، للإشارة إلى مصطلح في الصف الثاني ، العمود الثالث ، يمكنك تسميته R2C3.

جزء 2 من 4: تعلم عمليات حل نظام بمصفوفة

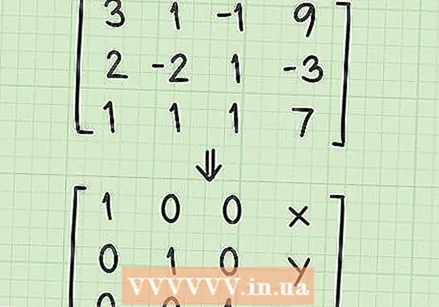1. افهم شكل مصفوفة الحل. قبل أن تبدأ في حل نظام المعادلات ، عليك أن تفهم ما ستفعله بالمصفوفة. في هذه المرحلة لديك مصفوفة تبدو كالتالي:
   • 3 1 -1 9
   • 2 -2 1 -3
   • 1 1 1 7
   • أنت تعمل مع عدد من العمليات الأساسية لإنشاء "مصفوفة الحل". ستبدو مصفوفة الحل كما يلي:
   • 1 0 0 x
   • 0 1 0 ذ
   • 0 0 1 ض
   • لاحظ أن المصفوفة تتكون من 1 في خط قطري مع 0 في جميع المسافات الأخرى باستثناء العمود الرابع. الأرقام الموجودة في العمود الرابع هي حل المتغيرات x و y و z.
2. استخدم الضرب العددي. أول أداة تحت تصرفك لحل نظام باستخدام مصفوفة هي الضرب القياسي. هذا ببساطة مصطلح يعني أنك تضرب العناصر الموجودة في صف من المصفوفة في رقم ثابت (وليس متغير). عند استخدام الضرب القياسي ، ضع في اعتبارك أنه يجب عليك ضرب كل حد في الصف بأكمله بأي رقم تحدده. إذا نسيت الحد الأول وضربت فقط ، فستحصل على الحل الخطأ. ومع ذلك ، لا يتعين عليك ضرب المصفوفة بأكملها في نفس الوقت. في الضرب العددي ، أنت تعمل فقط على صف واحد في كل مرة.
   • من الشائع استخدام الكسور في الضرب العددي لأنك غالبًا ما تريد الحصول على صف قطري من الآحاد. تعتاد على التعامل مع الكسور. سيكون من الأسهل أيضًا (لمعظم خطوات حل المصفوفة) أن تكون قادرًا على كتابة الكسور في صيغة غير صحيحة ، ثم تحويلها مرة أخرى إلى أعداد مختلطة من أجل الحل النهائي. لذلك ، من السهل التعامل مع الرقم 1 2/3 إذا كتبته على أنه 5/3.
   • على سبيل المثال ، يبدأ الصف الأول (R1) من مثالنا بالمصطلحات [3،1، -1،9]. يجب أن تحتوي مصفوفة الحل على 1 في الموضع الأول من الصف الأول. من أجل "تغيير" 3 إلى 1 ، يمكننا ضرب الصف بأكمله في 1/3. يؤدي هذا إلى إنشاء R1 الجديد لـ [1،1 / 3، -1 / 3،3].
   • تأكد من ترك أي علامات سلبية في مكانها.
3. استخدم جمع الصف أو طرح الصف. الأداة الثانية التي يمكنك استخدامها هي إضافة أو طرح صفين من المصفوفة. لإنشاء حدود 0 في مصفوفة الحل ، يجب عليك إضافة أو طرح الأرقام للوصول إلى 0. على سبيل المثال ، إذا كانت R1 مصفوفة [1،4،3،2] وكانت R2 هي [1،3،5،8] ، فيمكنك طرح الصف الأول من الصف الثاني وإنشاء صف جديد [0 ، -1 ، 2.6] ، لأن 1-1 = 0 (العمود الأول) ، 3-4 = -1 (العمود الثاني) ، 5-3 = 2 (العمود الثالث) ، و8-2 = 6 (العمود الرابع). عند إجراء إضافة صف أو طرح صف ، أعد كتابة النتيجة الجديدة بدلاً من الصف الذي بدأت به. في هذه الحالة سنقوم باستخراج الصف 2 وإدخال الصف الجديد [0، -1،2،6].
   • يمكنك استخدام تدوين مختصر وإعلان هذا الإجراء على أنه R2-R1 = [0، -1،2،6].
   • تذكر أن الجمع والطرح هما مجرد شكلين متعارضين لنفس العملية. فكر في الأمر على أنه جمع رقمين أو طرح العكس. على سبيل المثال ، إذا بدأت بالمعادلة البسيطة 3-3 = 0 ، يمكنك التفكير في هذا على أنه مشكلة إضافة 3 + (- 3) = 0. النتيجة هي نفسها. يبدو هذا بسيطًا ، ولكن من الأسهل أحيانًا النظر في المشكلة بشكل أو بآخر. فقط راقب علاماتك السلبية.
4. اجمع بين إضافة الصف والضرب القياسي في خطوة واحدة. لا يمكنك توقع تطابق المصطلحات دائمًا ، لذا يمكنك استخدام إضافة أو طرح بسيط لإنشاء 0 في المصفوفة الخاصة بك. في كثير من الأحيان سيكون عليك إضافة (أو طرح) مضاعف من صف آخر. للقيام بذلك ، عليك أولاً إجراء الضرب القياسي ، ثم إضافة تلك النتيجة إلى الصف الهدف الذي تحاول تغييره.
   • افترض؛ أن هناك صف 1 من [1،1،2،6] وصف 2 من [2،3،1،1]. تريد مصطلح 0 في العمود الأول من R2. أي أنك تريد تغيير 2 إلى 0. للقيام بذلك ، يجب عليك طرح 2. يمكنك الحصول على 2 بضرب الصف 1 أولاً في الضرب القياسي 2 ، ثم طرح الصف الأول من الصف الثاني. باختصار ، يمكن كتابة هذا كـ R2-2 * R1. أولاً ، اضرب R1 في 2 لتحصل على [2،2،4،12]. ثم اطرح هذا من R2 لتحصل على [(2-2) ، (3-2) ، (1-4) ، (1-12)]. بسّط هذا وستكون R2 الجديدة الخاصة بك [0،1 ، -3 ، -11].
5. انسخ الصفوف التي تظل دون تغيير أثناء العمل. أثناء عملك على المصفوفة ، ستقوم بتغيير صف واحد في كل مرة ، إما عن طريق الضرب القياسي ، أو إضافة الصف ، أو طرح الصف ، أو مجموعة من الخطوات. عند تغيير أحد الصفوف ، تأكد من نسخ الصفوف الأخرى من المصفوفة في شكلها الأصلي.
   • يحدث خطأ شائع عند إجراء عملية الضرب والجمع معًا في نقلة واحدة. على سبيل المثال ، لنفترض أنك بحاجة لطرح R1 من R2 مرتين. عندما تضرب R1 في 2 للقيام بهذه الخطوة ، تذكر أن R1 لا يتغير في المصفوفة. ما عليك سوى إجراء الضرب لتغيير R2. قم أولاً بنسخ R1 في شكلها الأصلي ، ثم قم بإجراء التغيير على R2.
6. أولا العمل من أعلى إلى أسفل. لحل النظام ، أنت تعمل في نمط منظم للغاية ، بشكل أساسي "حل" مصطلح واحد من المصفوفة في كل مرة. سيبدو تسلسل مصفوفة من ثلاثة متغيرات كما يلي:
   • 1. اجعل الرقم 1 في الصف الأول ، العمود الأول (R1C1).
   • 2. اجعل الرقم 0 في الصف الثاني ، العمود الأول (R2C1).
   • 3. اجعل الرقم 1 في الصف الثاني والعمود الثاني (R2C2).
   • 4. اكتب 0 في الصف الثالث ، العمود الأول (R3C1).
   • 5. اكتب 0 في الصف الثالث ، العمود الثاني (R3C2).
   • 6. اجعل الرقم 1 في الصف الثالث والعمود الثالث (R3C3).
7. اعملي من الأسفل إلى الأعلى. في هذه المرحلة ، إذا قمت بالخطوات بشكل صحيح ، فأنت في منتصف الحل. يجب أن يكون لديك خط قطري من 1 ، مع وجود 0 أسفله. الأرقام الموجودة في العمود الرابع لا تهم في هذه المرحلة. الآن تعود إلى القمة على النحو التالي:
   • قم بإنشاء 0 في الصف الثاني والعمود الثالث (R2C3).
   • قم بإنشاء 0 في الصف الأول والعمود الثالث (R1C3).
   • قم بإنشاء 0 في الصف الأول والعمود الثاني (R1C2).
8. تحقق مما إذا كنت قد أنشأت مصفوفة الحل. إذا كان عملك صحيحًا ، فقد قمت بإنشاء مصفوفة الحل مع 1 في خط قطري من R1C1 و R2C2 و R3C3 و 0 في المواضع الأخرى للأعمدة الثلاثة الأولى. الأرقام الموجودة في العمود الرابع هي الحلول لنظامك الخطي.

جزء 3 من 4: دمج الخطوات لحل المجرة

1. ابدأ بنظام مثال من المعادلات الخطية. لممارسة هذه الخطوات ، لنبدأ بالنظام الذي استخدمناه سابقًا: 3x + y-z = 9 ، 2x-2y + z = -3 ، و x + y + z = 7. إذا كتبت هذا في مصفوفة ، فلديك R1 = [3،1 ، -1،9] ، R2 = [2 ، -2،1 ، -3] ، و R3 = [1،1،1،7].
2. أنشئ 1 في الموضع الأول R1C1. لاحظ أن R1 يبدأ بـ 3 في هذه المرحلة ، وعليك تغييره إلى 1. يمكنك القيام بذلك عن طريق الضرب القياسي ، بضرب جميع الحدود الأربعة لـ R1 في 1/3. باختصار ، يمكنك الكتابة كـ R1 * 1/3. هذا يعطي نتيجة جديدة لـ R1 إذا كانت R1 = [1،1 / 3، -1 / 3،3]. انسخ R2 و R2 ، بدون تغيير ، عندما تكون R2 = [2، -2،1، -3] و R3 = [1،1،1،7].
   • لاحظ أن الضرب والقسمة ليسا سوى دالات معكوسة لبعضهما البعض. يمكننا القول إننا نضرب في 1/3 أو نقسم على 3 دون تغيير النتيجة.
3. قم بإنشاء 0 في الصف الثاني ، العمود الأول (R2C1). في هذه المرحلة ، R2 = [2، -2،1، -3]. للاقتراب من مصفوفة الحل ، تحتاج إلى تغيير المصطلح الأول من 2 إلى 0. يمكنك القيام بذلك عن طريق طرح ضعف قيمة R1 ، نظرًا لأن R1 يبدأ بـ 1. باختصار ، العملية R2-2 * R1. تذكر أنك لا تغير R1 ، فقط اعمل معها. لذا ، أول نسخة R1 إذا كانت R1 = [1،1 / 3، -1 / 3،3]. ثم إذا ضاعفت كل حد من R1 ، فستحصل على 2 * R1 = [2،2 / 3، -2 / 3،6]. أخيرًا ، اطرح هذه النتيجة من R2 الأصلي لتحصل على R2 الجديد. مصطلح العمل حسب المصطلح ، يصبح هذا الطرح (2-2) ، (-2-2 / 3) ، (1 - (- 2/3)) ، (-3-6). نبسطها إلى R2 الجديد = [0، -8 / 3،5 / 3، -9]. لاحظ أن المصطلح الأول هو 0 (مهما كان هدفك).
   • اكتب الصف 3 (الذي لم يتغير) بالشكل R3 = [1،1،1،7].
   • كن حذرًا عند طرح الأرقام السالبة للتأكد من بقاء الإشارات صحيحة.
   • الآن دعنا أولًا نترك الكسور في صورتها غير الصحيحة. هذا يجعل الخطوات اللاحقة للحل أسهل. يمكنك تبسيط الكسور في الخطوة الأخيرة من المسألة.
4. قم بإنشاء 1 في الصف الثاني ، العمود الثاني (R2C2). للاستمرار في تشكيل الخط المائل للآحاد ، يجب عليك تحويل الحد الثاني -8/3 إلى 1. افعل ذلك بضرب الصف بأكمله في مقلوب هذا الرقم (-3/8). رمزياً ، هذه الخطوة هي R2 * (- 3/8). الصف الثاني الناتج هو R2 = [0.1، -5 / 8.27 / 8].
   • لاحظ أنه إذا بدأ النصف الأيسر من الصف في تشابه الحل مع 0 و 1 ، فقد يبدأ النصف الأيمن في الظهور بشكل قبيح ، مع وجود كسور غير صحيحة. فقط اتركهم لما هم عليه الآن.
   • لا تنسَ الاستمرار في نسخ الصفوف التي لم تمسها ، لذا R1 = [1،1 / 3، -1 / 3،3] و R3 = [1،1،1،7].
5. قم بإنشاء 0 في الصف الثالث ، العمود الأول (R3C1). ينتقل تركيزك الآن إلى الصف الثالث ، R3 = [1،1،1،7]. لجعل 0 في الموضع الأول ، يجب عليك طرح 1 من 1 حاليًا في هذا الموضع. إذا نظرت لأعلى ، ستجد 1 في الموضع الأول من R1. لذلك تحتاج فقط إلى طرح R1 من R3 للحصول على النتيجة التي تريدها. مصطلح العمل للمصطلح ، يصبح (1-1) ، (1-1 / 3) ، (1 - (- 1/3)) ، (7-3). يمكن بعد ذلك تبسيط هذه المشكلات الأربع الصغيرة إلى R3 الجديد = [0.2 / 3.4 / 3.4].
   • استمر في النسخ على طول R1 = [1.1 / 3 ، -1 / 3.3] و R2 = [0.1 ، -5 / 8.27 / 8]. تذكر أنك تقوم بتغيير صف واحد فقط في كل مرة.
6. اجعل الرقم 0 في الصف الثالث والعمود الثاني (R3C2). هذه القيمة حاليًا 2/3 ، ولكن يجب تحويلها إلى 0. للوهلة الأولى ، يبدو أنه يمكنك طرح قيم R1 بمقدار الضعف ، لأن العمود المقابل لـ R1 يحتوي على 1/3. ومع ذلك ، إذا قمت بمضاعفة وطرح جميع قيم R1 ، فإن الرقم 0 في العمود الأول من R3 يتغير ، وهو ما لا تريده. سيكون هذا خطوة إلى الوراء في الحل الخاص بك. لذلك عليك العمل مع مزيج من R2. يؤدي طرح 2/3 من R2 إلى إنشاء 0 في العمود الثاني ، دون تغيير العمود الأول. باختصار ، هذا هو R3-2 / 3 * R2. تصبح المصطلحات الفردية (0-0) ، (2 / 3-2 / 3) ، (4/3 - (- 5/3 * 2/3)) ، (4-27 / 8 * 2/3) . ثم يعطي التبسيط R3 = [0،0،42 / 24،42 / 24].
7. قم بإنشاء 1 في الصف الثالث والعمود الثالث (R3C3). هذا هو الضرب البسيط في مقلوب الرقم الذي يقوله. القيمة الحالية هي 42/24 ، لذا يمكنك الضرب في 24/42 للحصول على القيمة التي تريدها 1. لاحظ أن كلا الحدين الأولين هما 0 ، لذا فإن أي عملية ضرب تظل 0. القيمة الجديدة لـ R3 = [0،0،1،1].
   • لاحظ أن الكسور التي بدت معقدة للغاية في الخطوة السابقة بدأت بالفعل في الحل.
   • تابع مع R1 = [1.1 / 3 ، -1 / 3.3] و R2 = [0.1 ، -5 / 8.27 / 8].
   • لاحظ أنه في هذه المرحلة يكون لديك قطري الآحاد لمصفوفة الحل. ما عليك سوى تحويل ثلاثة عناصر من المصفوفة إلى أصفار لإيجاد الحل.
8. قم بإنشاء 0 في الصف الثاني ، العمود الثالث. R2 حاليًا هي [0.1، -5 / 8.27 / 8] ، بقيمة -5/8 في العمود الثالث. يجب عليك تحويله إلى 0. هذا يعني أنه يجب عليك إجراء بعض العمليات باستخدام R3 والتي تتكون من إضافة 5/8. نظرًا لأن العمود الثالث المقابل لـ R3 هو 1 ، يجب عليك ضرب جميع قيم R3 في 5/8 وإضافة النتيجة إلى R2. باختصار هذا هو R2 + 5/8 * R3. مصطلح هذا هو R2 = (0 + 0) ، (1 + 0) ، (-5 / 8 + 5/8) ، (27/8 + 5/8). يمكن تبسيط هذا إلى R2 = [0،1،0،4].
   • ثم انسخ R1 = [1،1 / 3، -1 / 3،3] و R3 = [0،0،1،1].
9. قم بإنشاء 0 في الصف الأول والعمود الثالث (R1C3). الصف الأول حاليًا هو R1 = [1،1 / 3، -1 / 3،3]. يجب عليك تحويل -1/3 في العمود الثالث إلى 0 ، باستخدام مزيج من R3. لا تريد استخدام R2 ، لأن 1 في العمود الثاني من R2 قد يغير R1 بطريقة خاطئة. لذلك تضرب R3 * 1/3 وتضيف النتيجة إلى R1. تدوين هذا هو R1 + 1/3 * R3. ينتج عن مصطلح تفصيل المصطلح R1 = (1 + 0) ، (1/3 + 0) ، (-1 / 3 + 1/3) ، (3 + 1/3). يمكنك تبسيط هذا إلى R1 جديد = [1،1 / 3،0،10 / 3].
   • انسخ R2 دون تغيير = [0،1،0،4] و R3 = [0،0،1،1].
10. اجعل الرقم 0 في الصف الأول والعمود الثاني (R1C2). إذا تم كل شيء بشكل صحيح ، فيجب أن تكون هذه هي الخطوة الأخيرة. يجب عليك تحويل 1/3 في العمود الثاني إلى 0. يمكنك الحصول على هذا بضرب وطرح R2 * 1/3. باختصار ، هذا هو R1-1 / 3 * R2. النتيجة هي R1 = (1-0) ، (1 / 3-1 / 3) ، (0-0) ، (10 / 3-4 / 3). التبسيط ثم يعطي R1 = [1،0،0،2].
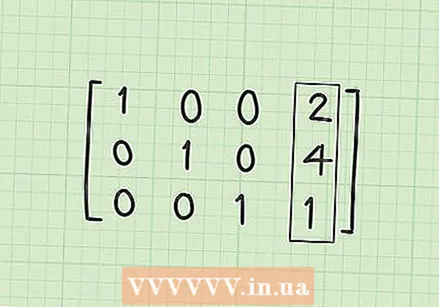11. ابحث عن مصفوفة الحل. في هذه المرحلة ، إذا سارت الأمور على ما يرام ، فستحصل على الصفوف الثلاثة R1 = [1،0،0،2] ، R2 = [0،1،0،4] و R3 = [0،0،1،1] يكون لديك. لاحظ أنك إذا كتبت هذا في نموذج مصفوفة الكتلة مع وجود صفوف واحدة فوق الأخرى ، فسيكون لديك قطري 1 مع 0 أبعد ، والحلول الخاصة بك في العمود الرابع. يجب أن تبدو مصفوفة الحل كما يلي:
    • 1 0 0 2
    • 0 1 0 4
    • 0 0 1 1
12. فهم الحل الخاص بك. بعد تحويل المعادلات الخطية إلى مصفوفة ، تضع معاملات x في العمود الأول ، ومعاملات y في العمود الثاني ، ومعاملات z في العمود الثالث. إذا كنت تريد إعادة كتابة المصفوفة إلى المعادلات مرة أخرى ، فإن هذه الأسطر الثلاثة للمصفوفة تعني في الواقع المعادلات الثلاث 1x + 0y + 0z = 2 ، 0x + 1y + 0z = 4 ، و 0 x + 0y + 1z = 1. نظرًا لأنه يمكننا شطب حدي 0 وعدم الحاجة إلى كتابة المعاملات 1 ، فإن هذه المعادلات الثلاث تبسط للحل ، x = 2 ، y = 4 ، و z = 1. هذا هو حل نظام المعادلات الخطية.

جزء 4 من 4: فحص الحل

1. قم بتضمين الحلول في كل متغير في كل معادلة. من الجيد دائمًا التحقق من صحة حلك بالفعل. يمكنك القيام بذلك عن طريق اختبار نتائجك في المعادلات الأصلية.
   • كانت المعادلات الأصلية لهذه المسألة هي: 3x + y-z = 9 ، 2x-2y + z = -3 ، و x + y + z = 7. عندما تستبدل المتغيرات بقيمها التي وجدتها ، تحصل على 3 * 2 + 4-1 = 9 ، 2 * 2-2 * 4 + 1 = -3 ، و 2 + 4 + 1 = 7.
2. تبسيط أي مقارنة. نفذ العمليات في كل معادلة وفقًا للقواعد الأساسية للعمليات. يتم تبسيط المعادلة الأولى إلى 6 + 4-1 = 9 ، أو 9 = 9. يمكن تبسيط المعادلة الثانية إلى 4-8 + 1 = -3 ، أو -3 = -3. المعادلة الأخيرة هي ببساطة 7 = 7.
   • نظرًا لأن أي معادلة تُبسط إلى بيان رياضي حقيقي ، فإن الحلول الخاصة بك صحيحة. إذا كان أي من الحلول غير صحيح ، فتحقق من عملك مرة أخرى وابحث عن أي أخطاء. تحدث بعض الأخطاء الشائعة عند التخلص من علامات الطرح على طول الطريق أو الخلط بين الضرب والجمع للكسور.
3. اكتب الحلول النهائية الخاصة بك. بالنسبة لهذه المسألة المعطاة ، يكون الحل النهائي هو x = 2 ، و y = 4 ، و z = 1.

نصائح

• إذا كان نظام المعادلات الخاص بك معقدًا للغاية ، مع العديد من المتغيرات ، فقد تتمكن من استخدام آلة حاسبة بيانية بدلاً من القيام بالعمل يدويًا. للحصول على معلومات حول هذا الموضوع ، يمكنك أيضًا الرجوع إلى wikiHow.