المحتوى

• خطوات
• الطريقة 1 من 3: حساب ميل معادلة الخط المستقيم
• الطريقة 2 من 3: احسب الميل باستخدام نقطتين
• طريقة 3 من 3: استخدام حساب التفاضل لحساب الميل

يميز المنحدر زاوية ميل الخط المستقيم إلى محور الإحداثي (الميل يساوي عدديًا ظل هذه الزاوية). المنحدر موجود في معادلة الخط المستقيم ويستخدم في التحليل الرياضي للمنحنيات ، حيث يكون دائمًا مساويًا لمشتق دالة. لتسهيل فهم الميل ، تخيل أنه يؤثر على معدل تغير الوظيفة ، أي أنه كلما زادت قيمة المنحدر ، زادت قيمة الدالة (لنفس قيمة المتغير المستقل).

خطوات

الطريقة 1 من 3: حساب ميل معادلة الخط المستقيم

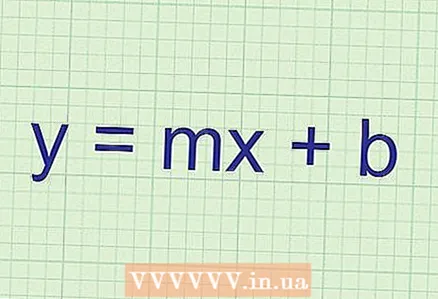1. 1 استخدم الميل لإيجاد زاوية الخط المستقيم على الإحداثية واتجاه ذلك الخط. حساب الميل سهل إلى حد ما إذا أعطيت لك معادلة الخط المستقيم. تذكر أنه في أي معادلة خط مستقيم:
   • لا دعاة
   • لا يوجد سوى متغيرين ، ليس أي منهما كسرًا (على سبيل المثال ، مثل ${ displaystyle { frac {1} {x}}}$)
   • معادلة الخط المستقيم لها الشكل ${ displaystyle y = kx + b}$، حيث k و b معاملات عددية (على سبيل المثال ، 3 ، 10 ، -12 ، ${ displaystyle { frac {4} {3}}}$).
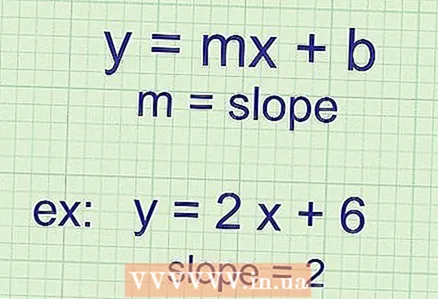2. 2 لإيجاد الميل ، عليك إيجاد قيمة k (معامل عند "x"). إذا كانت المعادلة المعطاة لك لها الشكل ${ displaystyle y = kx + b}$، ثم للعثور على المنحدر ، ما عليك سوى إلقاء نظرة على الرقم الموجود أمام "x". لاحظ أن k (الميل) يكون دائمًا عند المتغير المستقل (في هذه الحالة ، "x"). إذا كنت مرتبكًا ، فراجع الأمثلة التالية:
   • ${ displaystyle y = 2x + 6}$
     • المنحدر = 2
   • ${ displaystyle y = 2-x}$
     • المنحدر = -1
   • ${ displaystyle y = { frac {3} {8}} x-10}$
     • المنحدر = ${ displaystyle { frac {3} {8}}}$
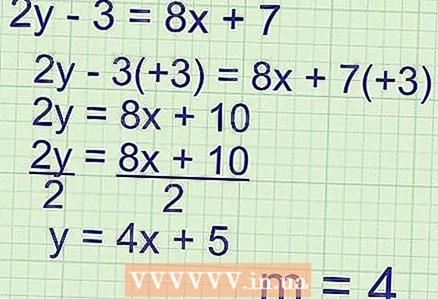3. 3 إذا كانت المعادلة المعطاة لك لها شكل آخر غير ذ=كx+ب{ displaystyle y = kx + b}، اعزل المتغير التابع. في معظم الحالات ، يتم الإشارة إلى المتغير التابع بـ "y" ، ولعزله ، يمكنك إجراء عمليات الجمع والطرح والضرب وغيرها. تذكر أنه يجب إجراء أي عملية حسابية على جانبي المعادلة (حتى لا تغير قيمتها الأصلية). تحتاج إلى إحضار أي معادلة معطاة لك في النموذج ${ displaystyle y = kx + b}$... لنفكر في مثال:
   • أوجد ميل المعادلة ${ displaystyle 2y-3 = 8x + 7}$
   • من الضروري إحضار هذه المعادلة إلى النموذج ${ displaystyle y = kx + b}$:
     • ${ displaystyle 2y-3 (+3) = 8x + 7 (+3)}$
     • ${ displaystyle 2y = 8x + 10}$
     • ${ displaystyle { frac {2y} {2}} = { frac {8x + 10} {2}}}$
     • ${ displaystyle y = 4x + 5}$
   • إيجاد المنحدر:
     • المنحدر = ك = 4

الطريقة 2 من 3: احسب الميل باستخدام نقطتين

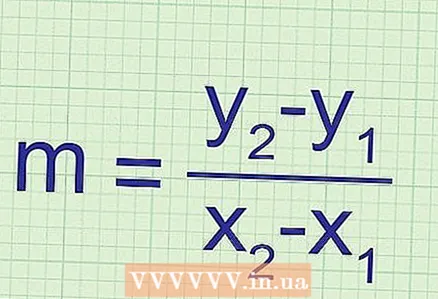1. 1 استخدم الرسم البياني والنقطتين لحساب الميل. إذا أعطيت للتو رسمًا بيانيًا لدالة (بدون معادلة) ، فلا يزال بإمكانك إيجاد الميل. للقيام بذلك ، تحتاج إلى إحداثيات أي نقطتين على هذا الرسم البياني ؛ يتم استبدال الإحداثيات في الصيغة: ${ displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}$... لتجنب الأخطاء عند حساب الميل ، تذكر ما يلي:
   • إذا كان الرسم البياني يتزايد ، فإن الميل يكون موجبًا.
   • إذا كان الرسم البياني يتناقص ، فإن الميل يكون سالبًا.
   • كلما زادت قيمة المنحدر ، كان الرسم البياني أكثر انحدارًا (والعكس صحيح).
   • ميل الخط المستقيم الموازي لمحور الإحداثي يساوي 0.
   • لا يوجد ميل للخط المستقيم الموازي للإحداثيات (إنه غير محدود).
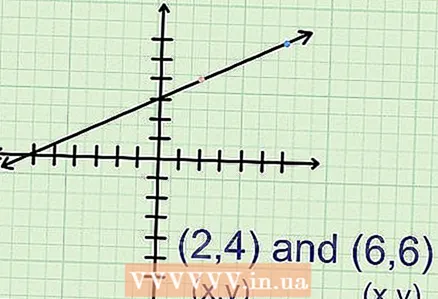2. 2 أوجد إحداثيات نقطتين. على الرسم البياني ، حدد أي نقطتين وابحث عن إحداثياتهما (س ، ص). على سبيل المثال ، النقطتان أ (2.4) وب (6.6) على الرسم البياني.
   • في زوج من الإحداثيات ، يتوافق الرقم الأول مع "س" والثاني مع "ص".
   • كل قيمة "x" تتوافق مع قيمة معينة "y".
3. 3 يساوي x₁، ذ₁، س₂، ذ₂ للقيم المقابلة. في مثالنا بالنقطتين A (2،4) و B (6،6):
   • x₁: 2
   • ذ₁: 4
   • x₂: 6
   • ذ₂: 6
4. 4 عوّض بالقيم التي تم العثور عليها في صيغة الميل. للعثور على المنحدر ، يتم استخدام إحداثيات نقطتين ويتم استخدام الصيغة التالية: ${ displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}$... عوض عن إحداثيات نقطتين.
   • نقطتان: أ (2.4) وب (6.6).
   • استبدل إحداثيات النقاط في الصيغة:
     • ${ displaystyle { frac {6-4} {6-2}}}$
   • تبسيط للحصول على إجابة محددة:
     • ${ displaystyle { frac {2} {4}} = { frac {1} {2}}}$ = المنحدر
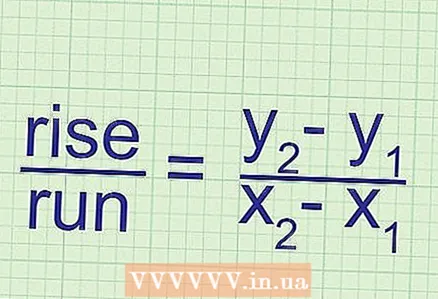5. 5 شرح جوهر الصيغة. الميل يساوي نسبة التغيير في إحداثي "ص" (نقطتان) إلى التغيير في إحداثي "س" (نقطتان). تغيير التنسيق هو الفرق بين قيم الإحداثي المقابل للنقطتين الأولى والثانية.
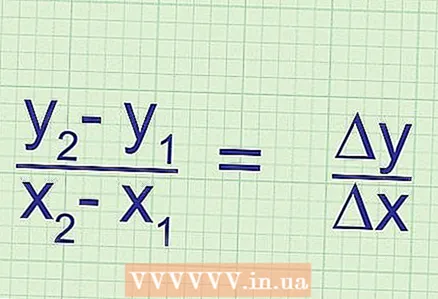6. 6 نوع آخر من المعادلات لحساب الميل. الصيغة القياسية لحساب الميل هي: k = ${ displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}$... ولكن يمكن أن يكون بالشكل التالي: k = Δy / Δx ، حيث Δ هو الحرف اليوناني "دلتا" للدلالة على الاختلاف في الرياضيات. أي Δx = x_2 - x_1 و y = y_2 - y_1.

طريقة 3 من 3: استخدام حساب التفاضل لحساب الميل

1. 1 تعلم أن تأخذ المشتقات من الوظائف. يميز المشتق معدل تغير دالة عند نقطة معينة على الرسم البياني لهذه الوظيفة. في هذه الحالة ، يمكن أن يكون الرسم البياني إما خطًا مستقيمًا أو خطًا منحنيًا. أي أن المشتق يميز معدل تغير الوظيفة في لحظة معينة من الزمن. تذكر القواعد العامة التي يتم من خلالها استخدام المشتقات ، وبعد ذلك فقط انتقل إلى الخطوة التالية.
   • اقرأ المقال كيف تأخذ المشتق.
   • كيفية أخذ أبسط المشتقات ، على سبيل المثال ، مشتق من المعادلة الأسية ، موصوف في هذه المقالة. ستستند الحسابات المقدمة في الخطوات التالية إلى الطرق الموضحة فيها.
2. 2 تعلم كيفية التمييز بين المسائل التي يحتاج فيها الميل إلى أن يُحسب من حيث مشتق الدالة. في المسائل ، لا يُقترح دائمًا إيجاد ميل أو مشتق دالة. على سبيل المثال ، قد يُطلب منك إيجاد معدل تغير دالة عند النقطة أ (س ، ص). قد يُطلب منك أيضًا إيجاد ميل المماس عند النقطة أ (س ، ص). في كلتا الحالتين ، من الضروري أخذ مشتق الوظيفة.
   • على سبيل المثال ، أوجد ميل دالة ${ displaystyle f (x) = 2x ^ {2} + 6x}$ عند النقطة أ (4.2).
   • غالبًا ما يتم الإشارة إلى المشتق على أنه ${ displaystyle f ’(x)، y’،}$ أو ${ displaystyle { frac {dy} {dx}}}$
3. 3 خذ مشتق الوظيفة المعطاة لك. لا تحتاج إلى رسم رسم بياني هنا - ما عليك سوى معادلة الدالة. في مثالنا ، خذ مشتق الدالة ${ displaystyle f (x) = 2x ^ {2} + 6x}$... خذ المشتق وفقًا للطرق الموضحة في المقالة المذكورة أعلاه:
   • المشتق: ${ displaystyle f ’(x) = 4x + 6}$
4. 4 عوّض بإحداثيات النقطة المعطاة في المشتق المشتق لحساب الميل. مشتق الدالة يساوي الميل عند نقطة معينة. بمعنى آخر ، f '(x) هو ميل الوظيفة عند أي نقطة (x، f (x)). في مثالنا:
   • أوجد ميل الدالة ${ displaystyle f (x) = 2x ^ {2} + 6x}$ عند النقطة أ (4.2).
   • مشتق من الوظيفة:
     • ${ displaystyle f ’(x) = 4x + 6}$
   • عوّض بقيمة الإحداثي x لهذه النقطة:
     • ${ displaystyle f ’(x) = 4 (4) +6}$
   • أوجد المنحدر:
   • منحدر الوظيفة ${ displaystyle f (x) = 2x ^ {2} + 6x}$ عند النقطة A (4.2) تساوي 22.
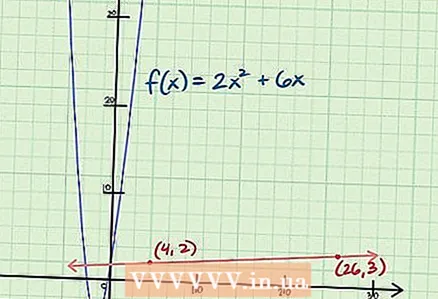5. 5 إذا أمكن ، تحقق من إجابتك على الرسم البياني. تذكر أنه قد لا يتم حساب الميل في كل نقطة. يأخذ حساب التفاضل في الاعتبار الدوال المعقدة والرسوم البيانية المعقدة ، حيث لا يمكن حساب الميل في كل نقطة ، وفي بعض الحالات لا تكمن النقاط على الرسوم البيانية على الإطلاق. إذا أمكن ، استخدم آلة حاسبة للرسوم البيانية للتحقق من أن الميل يتم حسابه بشكل صحيح للوظيفة المعطاة لك. بخلاف ذلك ، ارسم ظلًا للرسم البياني عند نقطة معينة وفكر فيما إذا كانت قيمة المنحدر التي وجدتها تتطابق مع ما تراه على الرسم البياني.
   • سيكون للماس نفس ميل الرسم البياني للوظيفة عند نقطة معينة.من أجل رسم ظل عند نقطة معينة ، انتقل إلى اليمين / اليسار على طول المحور X (في مثالنا ، 22 قيمة إلى اليمين) ، ثم لأعلى وحدة واحدة على المحور ص. حدد النقطة ، ثم قم بتوصيله بالنقطة المعطاة لك. في مثالنا ، قم بتوصيل النقاط عند الإحداثيات (4،2) و (26،3).